Baker-Campbell-Hausdorff formula
The Baker-Campbell-Hausdorff (BCH) formula provides a solution for $Z$ in the equation
$$ e^X e^Y = e^Z $$
where $X$ and $Y$ are possibly noncommutative elements in the Lie algebra of a Lie group.
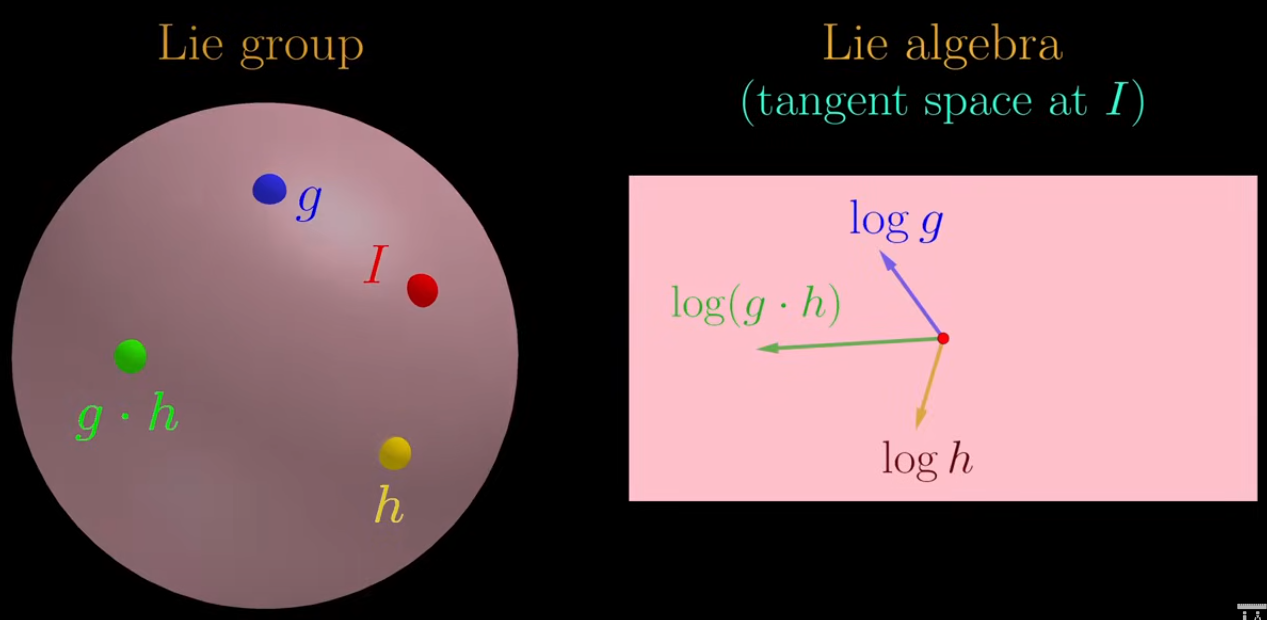
(picture from this video
The formula itself is an infinite series expansion:
$$ \log(e^X e^Y) = X + Y + \frac{1}{2}[X,Y] + \frac{1}{12}([X,[X,Y]] + [Y,[Y,X]]) + \dots $$Related: Zassenhaus formula.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: